
In den letzten Jahrzehnten hat das Interesse an historischen Stimmungen in wesentlichem Masse zugenommen. Die Erkenntnis hat sich durchgesetzt, dass zu einer Interpretation, die sich möglichst nahe an das Original halten will, auch die entsprechende Stimmung eines Instruments gehört. In Aufsätzen und Büchern werden dabei die Stimmungen meistens lediglich mit einer Anzahl von Zahlen präsentiert. Dabei ist es recht schwierig, sich aus diesen Zahlen eine Vorstellung von der Klangerscheinung dieser Stimmungen zu machen. Die hier präsentierten graphischen Darstellungen sollen helfen, verschiedene Stimmungen in ihren Auswirkungen auf die Reinheit der Akkorde zu überblicken und miteinander vergleichen zu können.
Dieses Kapitel dient dazu, die Grundlagen der Intervallproportionen und eines Feinmasses für die Intervallberechnungen zu geben. Wer sich hier darin auskennt, möge das Kapitel überspringen.
Die Natur der Intervalle bringt es mit sich, dass es unmöglich ist, alle Intervalle bei einem Tasteninstrument rein zu stimmen. Reine Quinten ziehen zu weite grosse Terzen nach sich, eine rein gestimmte grosse Terz bedingt zu enge Quinten. In den folgenden Erläuterungen wird darauf eingegangen.
Das Längenverhältnis zweier Pfeifen, die eine Oktave auseinanderliegen,
beträgt 2:1,
aus der Berechnung 8’:4’ = 2:1.
Das Längenverhältnis zweier Pfeifen, die eine Quinte auseinanderliegen,
beträgt 3:2,
aus der Berechnung
4’:2 2/3’ =
12/3’:8/3’ = 12:8 = 3:2.
Das Längenverhältnis zweier Pfeifen,
die eine grosse Terz auseinanderliegen, beträgt 5:4,
aus der Berechnung 2’:1 3/5’ =
10/5’:8/5’ = 10:8 = 5:4.
Frequenzen und Pfeifenlängen verhalten sich umgekehrt proportional. So entspricht z.B. doppelte Frequenz einer halben Pfeifenlänge.
Nun stellen wir uns eine Pfeife vor, die in ihrer Länge 80 cm (2 2/3’) misst, was bei einer offenen Prinzipalpfeife etwa dem Ton g entspricht. Nun gehen wir davon 2 Oktaven und eine grosse Terz aufwärts und darauf 4 Quinten abwärts wiederum zu g:
 |
||||||||
| Pfeifenlängen in cm | 80 | 40 | 20 | 16 | 24 | 36 | 54 | 81 |
Der Ton zu Beginn der Tonfolge entspricht also nicht genau dem Ton am Ende der Folge. Der kleine Unterschied beträgt 81:80. Dieser Unterschied heisst das syntonische Komma (oder didymisches Komma) und war bereits bei den Griechen im Altertum bekannt.
Werden Intervalle addiert, so multipliziert man die Längenverhältnisse der Pfeifen. Bei einer Subtraktion der Intervalle dividiert man die Verhältnisse. Die Formel zur Berechnung des syntonischen Kommas lautet somit:
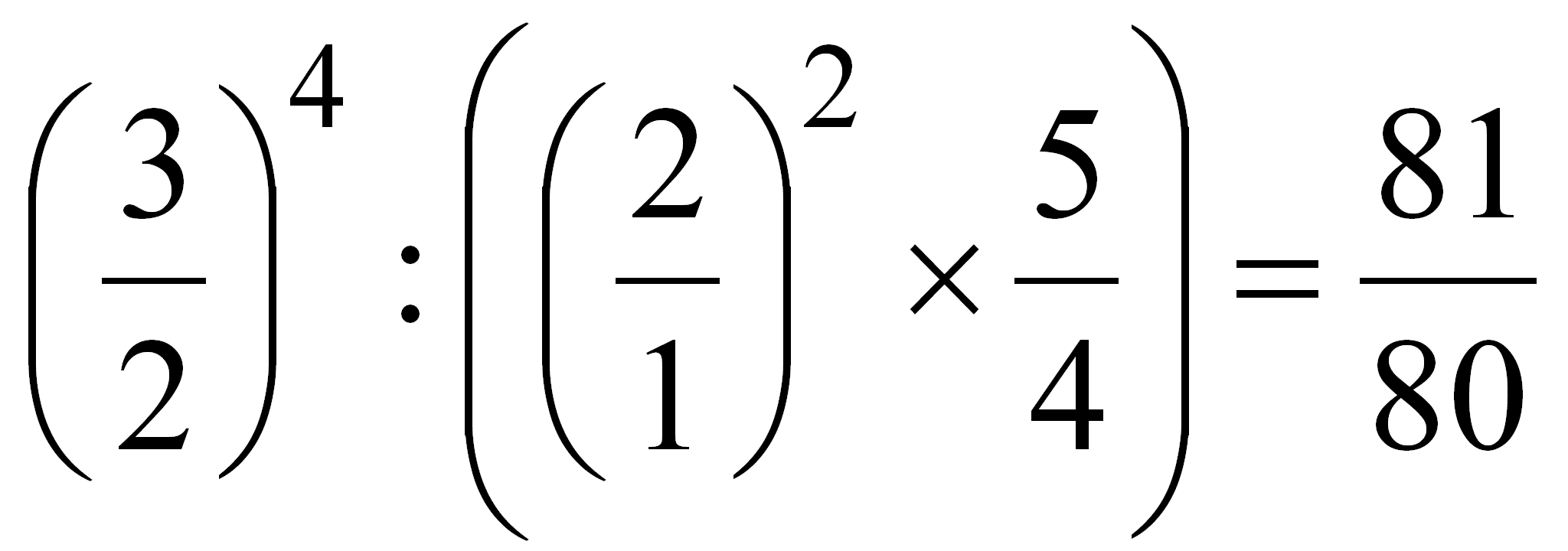
Zweitens gehen wir von einer Pfeife mit einer Länge von 524,4 cm aus, was ungefähr dem B2 (subkontra B) entspricht. Wir steigen 7 Oktaven nach aufwärts zum b””:
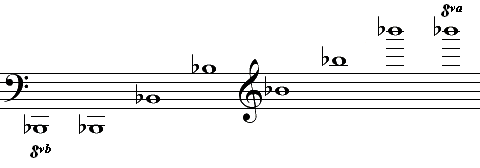 |
||||||||
| Pfeifenlängen in cm | 524,4 | 262,2 | 131,1 | 65,5 | 32.8 | 16.4 | 8,2 | 4,1 |
Anschliessend gehen wir 12 Quinten hinunter zum Ausgangspunkt zurück:
 |
||||||||||||
| Pfeifenlängen in cm | 6,1 | 9,2 | 13,8 | 20,7 | 31,1 | 46,7 | 70,0 | 105,0 | 157,5 | 236,5 | 354,3 | 531,4 |
Auch hier ergibt sich ein kleiner Unterschied, welcher das pythagoreische Komma genannt wird. Dieses beträgt 531441:524228, was ungefähr dem Verhältnis 74:73 entspricht. Das pythagoreische Komma ist somit etwas grösser als das syntonische Komma. Die Formel zur Berechnung des pythagoreischen Kommas lautet:
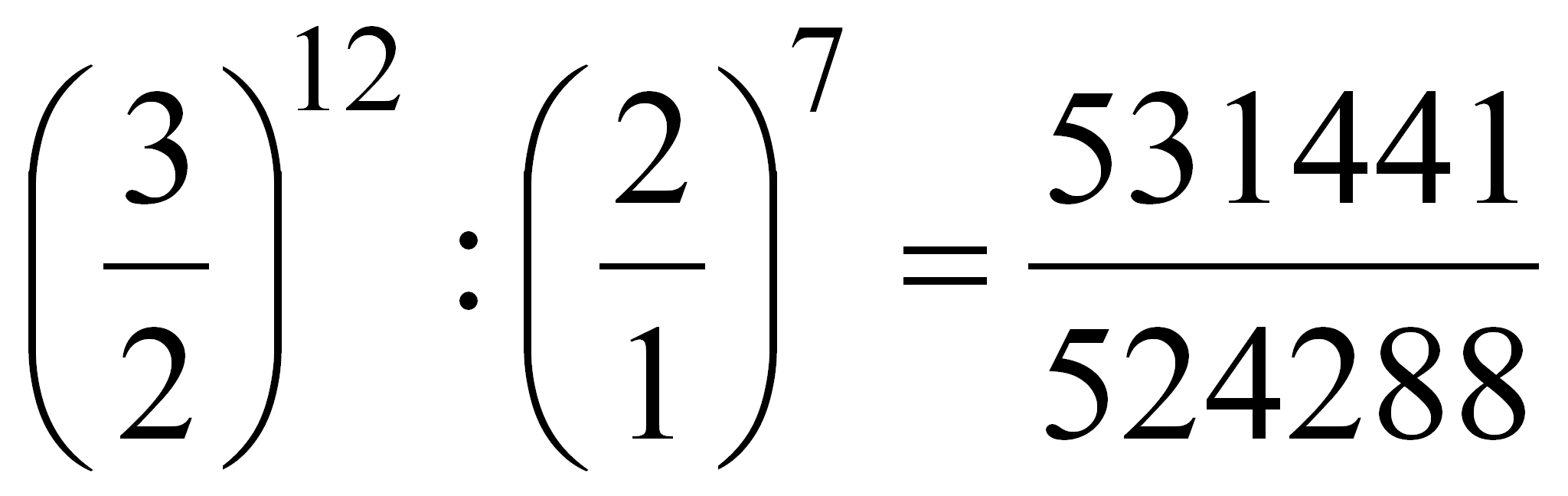
Das pythagoreische Komma ergibt sich aus der Teilung der Oktave in 12 Halbtöne. Die heute weitgehend gebräuchliche gleichstufige Stimmung teilt die Oktave in genau 12 gleich grosse Halbtöne ein. Das pythagoreische Komma wird so gleichmässig auf alle 12 Quinten des Quintenzirkels verteilt.
Drittens gehen wir von einer Pfeife mit der Länge von 125 cm aus, was ungefähr dem kleinen ces entspricht. Wir steigen 3 grosse Terzen nach oben und gehen eine Oktave nach unten zum grossen H:
 |
|||||
| Pfeifenlängen in cm | 125 | 100 | 80 | 64 | 128 |
Der Unterschied zwischen Ces und H ist grösser als die beiden erwähnten Kommata und heisst die kleine Diësis, mit dem Verhältnis 128:125. Die Formel zu ihrer Berechnung lautet:
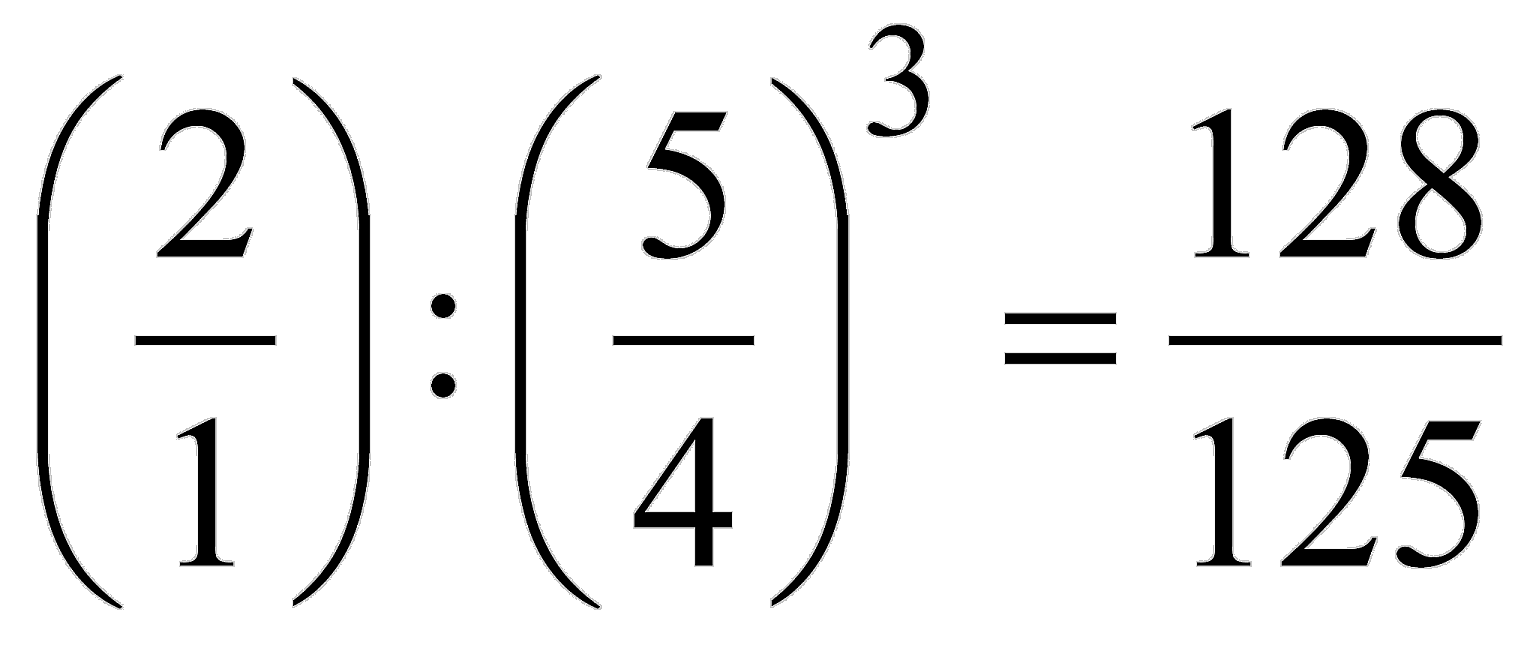
Die übliche Bezeichnung der Intervalle ist nicht ausreichend genau, um die präzise Stimmung eines Intervalls festzuhalten. Deswegen teilte ein englischer Physiker des 19. Jahrhunderts, John Ellis, die Oktave in 1200 gleiche Teile ein. Jeder Halbton beträgt in dieser Messung 100 Cent, sofern alle Halbtöne in demselben Abstand stehen (was in der gleichstufigen Temperatur der Fall ist).
Die rein gestimmten Quinten und grossen Terzen weichen leicht von den obigen Zahlen ab. So beträgt der Wert der rein gestimmten Quinte 701,955 Cent, gerundet 702 Cent. Der Wert der rein gestimmten grossen Terz beträgt 386,314 Cent, gerundet 386 Cent. Die rein gestimmte Quinte ist demzufolge um 2 Cent grösser als die gleichstufig temperierte Quinte, die rein gestimmte grosse Terz um 14 Cent kleiner als die gleichstufig temperierte grosse Terz. Das pythagoreische Komma beträgt 23,460 Cent, gerundet 24 Cent (12 × 2 Cent), das syntonische Komma 21,506 Cent, gerundet 22 Cent (4 × 2 Cent der Quintabweichung, dazu 14 Cent der Terzabweichung gegenüber der gleichstufigen Stimmung, oder 408 Cent (Wert der pythagoreischen grossen Terz aus 4 übereinanderliegenden reinen Quinten) minus 386 Cent (Wert der rein gestimmten grossen Terz) und der Wert der kleinen Diësis 41,059, gerundet 42 Cent (3 × 14 Cent der Terzabweichung).
Zusammenfassend lässt sich festhalten: Werden im Quintenzirkel alle Quinten rein gestimmt, ist der Schlusston um rund 24 Cent höher als der Anfangston (pythagoreisches Komma).
Werden 3 grosse Terzen rein gestimmt, ist der Schlusston um rund 42 Cent tiefer als der Anfangston (kleine Diësis).
Wird eine rein gestimmte grosse Terz in Zusammenhang mit vier aufeinanderfolgenden rein gestimmten Quinten gestellt, so beträgt der Unterschied rund 22 Cent (syntonisches Komma). Um die Nachbarschaft der Töne wiederherzustellen, sind die entsprechenden Oktaven abzuziehen.
In graphischer Darstellung ergibt sich folgendes Bild:
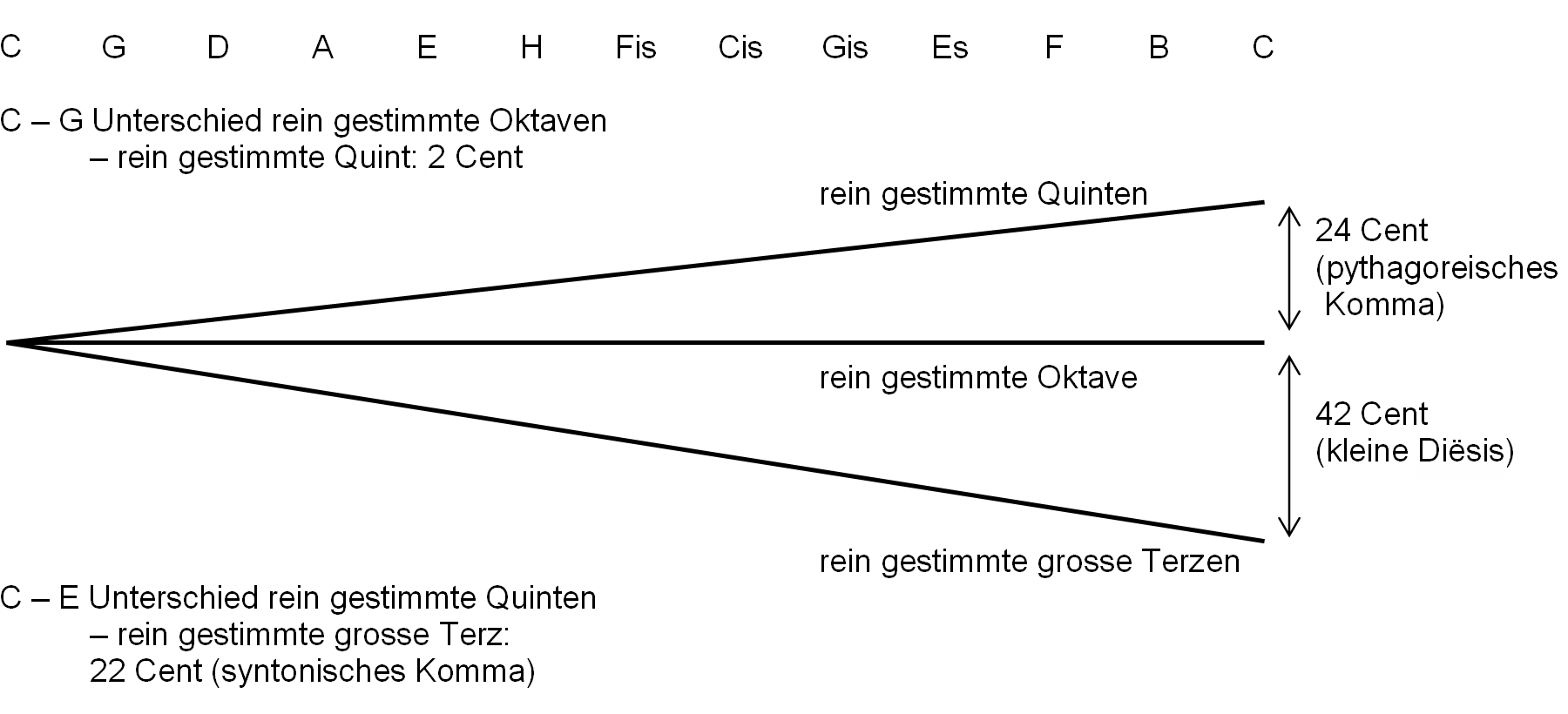
Bemerkungen zur obigen Darstellung:
Wird die Oktave in 12 gleiche Teile unterteilt (gleichstufige Stimmung), ergeben sich für die Quinte 700 Cent. Die rein gestimmte Quinte hat einen Wert von 702 Cent, daher resultiert der Unterschied bei C-G von 2 Cent.
Werden die Quinten rein gestimmt, ergibt sich bei der grossen Terz ein Wert von 408 Cent. Werden die grossen Terzen rein gestimmt, ergibt sich für diese ein Wert von 386 Cent. Der Unterschied beträgt 22 Cent, was dem Wert des syntonischen Kommas entspricht.
Es ist also unmöglich, alle Intervalle rein zu stimmen. In der Musikgeschichte finden sich viele verschiedene Stimmungen. Sie sind, in graphischer Darstellung und mit Kommentaren versehen, in dieser Website erstmals zusammengestellt.
Von ihrer Charakteristik lassen sich die Stimmungen in 7 Gruppen einteilen:
Für die Orgeln stellt sich nun die Frage nach einer geeigneten Stimmung.
Bei den meisten Orgeln lässt sich eine gewisse Literatur besser, eine andere weniger gut darstellen.
Persönlich möchte ich folgende Vorschläge geben:
Welche Stimmung aus der entsprechenden Gruppe genommen wird, kann durch Vergleichen der Stimmungen bestimmt werden.
Stimmungen für Cembalo:
Ausgangspunkt für die graphische Darstellung ist in der Waagrechten die gleichstufige Stimmung.
In der Senkrechten sind die rein gestimmten Quinten (Verhältnis 3/2)
und rein gestimmten grossen Terzen (Verhältnis 5/4) der Ausgangspunkt.
Töne mit positiver Abweichung sind oberhalb, solche mit negativer Abweichung
unterhalb der Waagrechten platziert.
Der Verlauf der ausgezogenen dunkelroten Linie zeigt die Abweichung der Töne
des Quintenzirkels von der gleichstufigen Stimmung.
Die einzelnen Töne sind mit dem Symbol
![]() markiert.
Die grossen Terzen sind mit dem Zeichen
markiert.
Die grossen Terzen sind mit dem Zeichen
![]() markiert
und mit einer gestrichelten blauen Linie verbunden.
Für die Darstellung der Quinten wird das Zeichen
markiert
und mit einer gestrichelten blauen Linie verbunden.
Für die Darstellung der Quinten wird das Zeichen
![]() verwendet;
sie sind mit einer strichpunktierten grünen Linie verbunden.
verwendet;
sie sind mit einer strichpunktierten grünen Linie verbunden.
Als Beispiel zeigen wir hier die Graphik der Stimmung Mersenne 1:
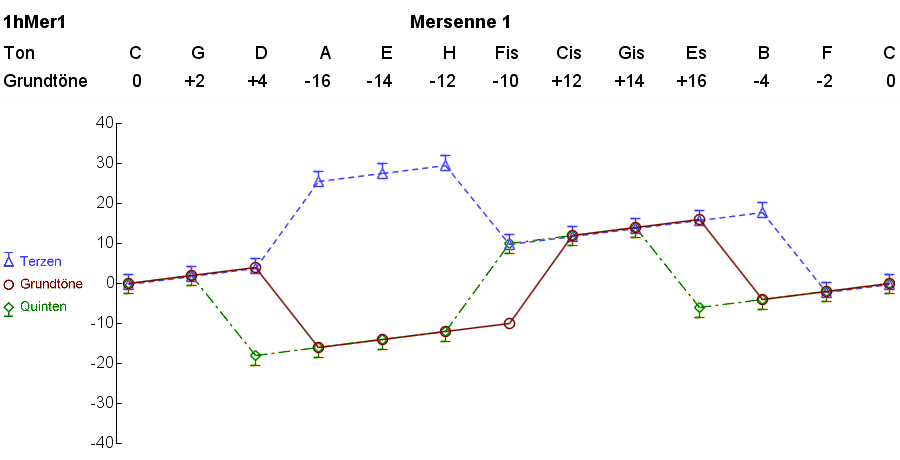
Bei diesen Graphiken lässt sich die Reinheit der Dur-Dreiklänge im Quintenzirkel gut ablesen. Je näher beisammen die Punkte des Grundtones, der Quinte und der grossen Terz liegen, umso reiner klingt der entsprechende Akkord. Drei Punkte, die sich überdecken, entsprechen einem reinen Dur-Dreiklang.
Jede beliebige, auch selbst entworfene Stimmung lässt sich auf diese Weise graphisch darstellen; damit wird die Auswirkung auf die Dur-Dreiklänge sichtbar.
Da die Dur-Dreiklänge empfindlicher auf Unreinheiten reagieren als die Moll-Dreiklänge, beschränkt sich die graphische Darstellung auf die Dur-Dreiklänge. Die Bezeichnung „Terzen“ in den Graphiken bedeutet also stets die grossen Terzen.
In Dur ist es sinnvoll, den Quintenzirkel von C bis C zu zeichnen. Die elektronischen Stimmgeräte gehen jedoch vom a aus. Deshalb sind in den Cent-Angaben auch die Abweichungen der Grundtöne gegenüber der gleichstufigen Stimmung vom a aus angegeben.
In einer Arbeit über Stimmungen erhebt sich unweigerlich die Frage der Genauigkeit der Angaben. Unser Gehör unterscheidet im besten Falle Werte von einem Cent Unterschied. So sind in dieser Arbeit alle Werte auf ein Cent auf- oder abgerundet. Dabei können sich auch Konflikte ergeben, wie das folgende Beispiel zeigt: 5,6 − 2,3 = 3,3, abgerundet 3. Mit Auf- und Abrundungen der gegebenen Zahlen: 6 − 2 = 4. Wird das Resultat 3 gewünscht, heisst die Rechung 5 − 2 = 3. Die Zunahme der Ungenauigkeit bei der Zahl 5,6 liegt bei 0,2 Cent, also deutlich unter der Schwelle des Hörbaren. In verschiedenen Publikationen wird deswegen mit ganzen Cent gerechnet; diese Genauigkeit kann für die Praxis als genügend angesehen werden. Bei der Frage, ob bei den Rundungen vom C oder vom A ausgegangen werden soll, wird dem C infolge der Graphiken dem Vorzug gegeben. So ist es möglich, dass sich im Vergleich zu von A ausgehenden Publikationen ein Unterschied von 1 Cent ergibt.
In verschiedenen Publikationen sind die Cent-Angaben mit Kommastellen versehen, wobei das Maximum bei nicht weniger als 9 Stellen liegt! Um dem Bedürfnis nach genaueren Angaben Genüge zu tun, sind unter der Bezeichnung „genauer“ diejenigen Stimmungen aufgeführt, bei denen in der angegebenen Literatur genauere Cent-Angaben vorliegen. Aus Platzgründen werden jedoch nur 2 Kommastellen angegeben.
Die einzelnen Seiten der Stimmungen sind wie folgt gegliedert:
Hier werden die rechnerischen Grundlagen erläutert, die zur Herstellung der Graphiken benutzt werden. Ausgangspunkt für die Graphik ist wie erwähnt die gleichstufige Stimmung. Sind die Centzahlen der einzelnen Töne von irgendeiner Stimmung bekannt, werden diese von den Centzahlen der gleichstufigen Stimmung abgezogen.
Sind die Abweichungen der Centzahlen von der Basis des Tones A bekannt, erhält man die Abweichungen der Centzahlen auf der Basis des Tones C, indem man von der Abweichung des entsprechenden Tones die Abweichung des Tones C abzieht.
Für die Abweichungen der Quinten zählt man die Abweichung des unteren Tones von der Abweichung des oberen Tones ab; davon wird noch die Zahl 2 abgezogen (diese Zahl ergibt sich aus dem Unterschied der rein gestimmten Quinte 702 Cent − gleichstufig temperierte Quinte 700 Cent).
Für die Abweichungen der grossen Terzen zählt man die Abweichung des unteren Tones von der Abweichung des oberen Tones ab; dazu wird noch die Zahl 14 addiert (diese Zahl ergibt sich aus dem Unterschied der rein gestimmten grossen Terz von 386 Cent und der gleichstufig temperierten Terz von 400 Cent).
Der Dichter Hermann Hesse schliesst ein Gedicht vom 4. April 1962 mit den Worten:
Gis und As, Es und Dis
Sind dem Ohr sie unterscheidbar?
Eine mögliche Antwort kann lauten:
In der gleichstufig temperierten Stimmung sind die Töne dem Ohr nicht unterscheidbar.
Je nach Stimmung können aber Gis höher oder tiefer als As, Es höher oder tiefer als Dis sein,
sind also dem Ohr unterscheidbar.
H. E. Frischknecht (2007)
Online-Version: J. Schmid (2013)